Circular orbits
After studying this section you should be able to:
- describe the forces acting on planets, moons and satellites
- explain how charged particles are accelerated in a cyclotron
This section cover the following topics
All planetary movement in the Solar System is anticlockwise, when viewed from above the North Pole. The further a planet is from the Sun, the slower the speed in its orbit. Although the orbits of the planets are ellipses, for most planets they are so close to circles that our understanding of circular motion can be applied.
Planets can be considered to be:
- moving at constant speed in a circle around the Sun
- accelerating towards the Sun with centripetal acceleration v2/r.
Mercury and Pluto have highly elliptical orbits, the other planets follow paths that are very close to being circles.
In space there are no resistive forces since the planets move through a vacuum. The only forces acting on them are gravitational. Gravitational attraction between a planet and the Sun provides the unbalanced force required to cause the centripetal acceleration.
The diagram shows the attractive forces between the Sun and a planet.
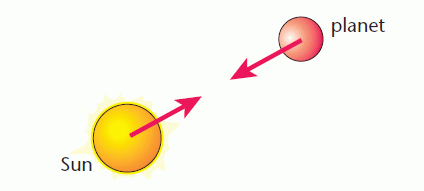
This diagram shows that the gravitational force on a planet acts at its centre of mass and is directed towards the Sun’s centre of mass.
The force on the planet is:
- equal in size and opposite in direction to that on the Sun
- at right angles to its direction of motion
- the unbalanced, centripetal force required to maintain circular motion.
By equating the gravitational force to mv2/r, it emerges that the orbital speed depends only on the orbital radius and not on the mass of the planet.
Asteroids in the asteroid belt, between Mars and Jupiter, have a wide range of masses but similar orbit times.
KEY POINT - The centripetal force required to keep a planet in a circular orbit is the gravitational force between the planet and the Sun:
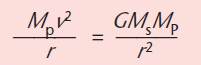
so v2r = GMs where Ms is the mass of the Sun and Mp is the mass of the planet.
The relationship between the orbital speed and radius of a planet can be applied to the orbit of a satellite around the Earth by replacing the mass of the Sun, Ms, with that of the Earth, ME. This enables the speed of a satellite to be calculated at any orbital radius.
The relationship also applies to the Earth’s natural satellite, the Moon.
Some communications satellites occupy geo-synchronous orbits. A satellite in a geo-synchronous orbit:
- orbits above the equator
- remains in the same position relative to the Earth’s surface
- has an orbit time of 24 hours.
The radius of a geo-synchronous orbit can be calculated from v2r = GME. As there are two unknowns in this equation, v can be written as 2πr/t to work out the value
of r.
Circular orbits in magnetic fields
When a charged particle moves at right angles to a magnetic field, the magnetic force on the particle is perpendicular to both its direction of motion and the magnetic field. This can result in circular motion.
The diagram shows the path and the force on an electron moving in a magnetic field directed into the paper.
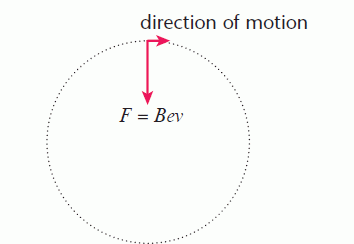
When applying Fleming’s rule to electrons, remember that the direction of the current is opposite to that of the electrons’ motion.
The electron follows a circular path, the magnetic force being the unbalanced force required to cause acceleration towards the centre of the circle. The radius of the circular path is proportional to the speed of the electron.
KEY POINT - When a charge Q moves in a circular path in a magnetic field of strength B:
BQv=mv2/r so BQ = mv/r
For an electron, Q = e, so the relationship is Be = mv/r
A cyclotron uses a magnetic field to force charged particles to move in a circular path, and an electric field to accelerate them as they travel around the circle. As the charged particles accelerate, the increase in speed results in an increase in the radius of the circle, so they spiral outwards.
A cyclotron consists of two D-shaped halves called dees. A magnetic field acting at right angles to the plane of the dees causes a beam of charged particles to follow a circular path. Particles such as protons and alpha particles are both suitable for use in cyclotrons.
Particles accelerated in a cyclotron are used to probe atomic nuclei and for treating some cancers.
The diagram shows the path of protons produced at the centre of the cyclotron.
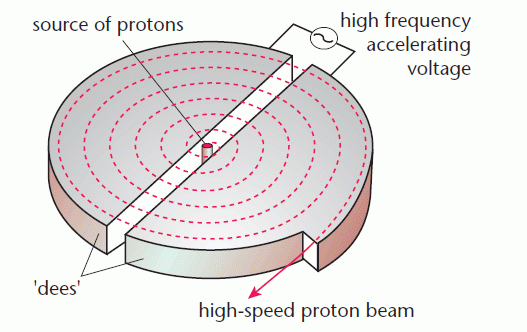
In a cyclotron:
- the beam of charged particles is accelerated as it passes from one dee into the other
- this occurs because of the alternating electric field which changes polarity so that it attracts the particles as they enter a dee
- the frequency of the alternating voltage must be equal to the frequency of rotation of the particles
- the radius of orbit increases as the particles accelerate.
The frequency of rotation of the charged particles in a cyclotron matches that of the accelerating voltage and does not depend on the speed of the particles. The value of the magnetic field strength can be adjusted to achieve the desired frequency.
If the frequency of the accelerating voltage is fixed, each orbit takes the same time. With an increase in the radius of successive orbits, the particles travel increasing distances in a given time period.
KEY POINT - The frequency of rotation of a charged particle in a cyclotron, f, is related to the magnetic field strength, B, by the expression:
f = BQ / 2πm where Q is the charge on a particle of mass m.
PROGRESS CHECK

