Photoelectric Effect

The Photoelectric effect provides evidence that electromagnetic waves have particle-like behaviour.

In the photoelectric effect, electrons are emitted from a metal’s surface when it absorbs electromagnetic radiation.

The diagram below shows this.

Image

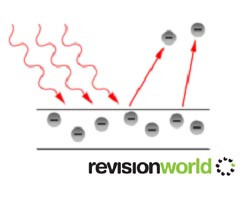
There are no electrons emitted below a certain frequency, called the threshold frequence, f_o , which is different for different metals.

Above this frequency, electrons are emitted with a range of kinetic energies up to a maximum, (½mv²)_max

Image

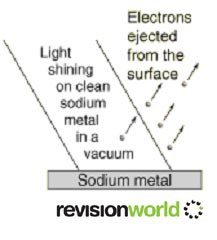
The wave model cannot explain the Photoelectric effect.

The explanation for this relies on the concept of the photon, a quantum packet of energy. So EM radiation is given by short bursts of energy.

The relationship between the energy of the photon, E, and its frequency is given by:

Image

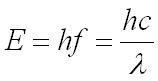
E = energy of the photon in joules, J

h = the Plank constant 6.63 x 10-34Js

f = frequency in hertz, Hz

c = speed of light 3.00 x 108 metres per second, ms-1

λ= wavelength in metres, m

The energy of a photon can be measured in Joules or Electronvolts.

One electronvolt is the energy transfer when an electron moves through a potential difference of 1 volt, given by: 1 eV = 1.60x10^-19 J

The minimum energy required for the electron to escape the metal is called the work function, Φ

If energy is less than Φ, then no emission occurs

Emission is possible when hf = Φ

The photoelectric equation relates the maximum kinetic energy of the emitted electrons to the work function and the energy of each photon: hf = Φ + (½mv²)

At the threshold frequency, the minimum frequency that can cause an emission is zero, so the equation becomes: hf_o = Φ