Forces and Elasticity

This section explains forces and elasticity covering, elastic and inelastic deformation, extension of spring and forces and extension’s linear relationship.

Elastic and Inelastic Deformation

Elastically Deformed

An object is said to be elastically deformed when it is stretched or compressed and returns to its original shape once the force is removed. This type of deformation occurs within the elastic limit of the material, where it can return to its original length or shape.

Examples of materials that undergo elastic deformation include:

• Rubber bands
• Springs (within their elastic limit)
• Steel wires (within certain limits)

Inelastically Deformed

An object is said to be inelastically deformed when it is stretched or compressed and does not return to its original shape or length when the force is removed. This occurs when the material is stretched beyond its elastic limit, causing permanent deformation.

Examples of inelastic deformation include:

• A plastic ruler that bends permanently
• A piece of clay that changes shape permanently when squeezed

Extension of a Spring

When a force is applied to a spring, it can stretch (extend) or compress, depending on the direction of the force. If the spring obeys Hooke's Law, the extension of the spring is directly proportional to the force applied, provided the limit of elasticity is not exceeded.

• The extension is the increase in the length of the spring compared to its original length.
• Compression is the decrease in length.

The relationship between the force applied and the extension is a key concept in elasticity.

Force of a Spring: Hooke's Law

Hooke’s Law states that the force needed to extend or compress a spring is directly proportional to the extension or compression, provided the elastic limit is not exceeded. This can be expressed mathematically as:

$$F = k \times \Delta x$$

Where:

• F is the force applied in Newtons (N).
• k is the spring constant (also called stiffness), measured in Newtons per metre (N/m).
• Δx (or $x$) is the extension or compression in metres (m).

Example:

A spring has a spring constant $k = 50 \, \text{N/m}$. If a force of 10 N is applied to stretch the spring, the extension of the spring can be calculated as follows:

$$F = k \times \Delta x$$

$$10 \, \text{N} = 50 \, \text{N/m} \times \Delta x$$

$$\Delta x = \frac{10}{50} = 0.2 \, \text{m}$$

So, the extension of the spring is 0.2 metres (or 20 cm).

Force and Extension: Linear Relationship

For springs that obey Hooke’s Law, the relationship between the force applied and the extension of the spring is linear. This means that if you double the force, the extension will also double, as long as the spring remains within its elastic limit.

Graph of Force vs. Extension

If you plot the force applied to a spring against its extension, the graph will be a straight line, indicating a linear relationship. The slope of this graph represents the spring constant (k), which measures the stiffness of the spring.

Image

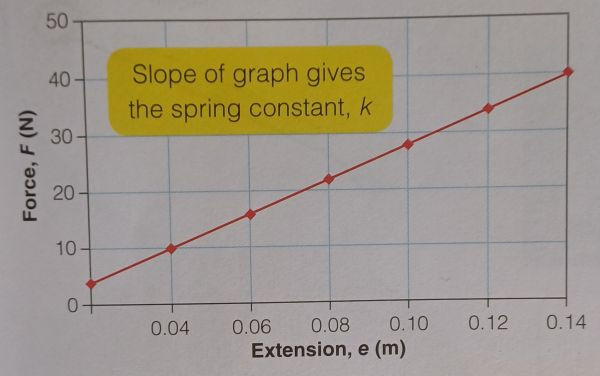
• If the graph is a straight line, it indicates that the spring obeys Hooke’s Law.
• If the graph starts to curve or bend, this means the spring has exceeded its elastic limit and no longer follows Hooke’s Law.

Elasticity describes how materials deform when forces are applied and return to their original shape when those forces are removed (elastic deformation). If the material doesn't return to its original shape, it is said to be inelastically deformed. Hooke’s Law gives us a formula to calculate the force required to stretch or compress a spring, showing that force is directly proportional to extension, if the spring operates within its elastic limit. Understanding the relationship between force and extension is crucial in understanding how elastic materials behave under force.