Transverse and Longitudinal Waves

This section explains transverse and longitudinal waves covering, transverse waves, longitudinal waves, wave movements, the properties of waves, wave speed, and the wave speed equation. 

Transverse Waves

Transverse waves are waves in which the oscillations (vibrations) occur perpendicular to the direction of wave travel. In other words, the particles of the medium move up and down (or side to side) while the wave itself moves horizontally.

Image

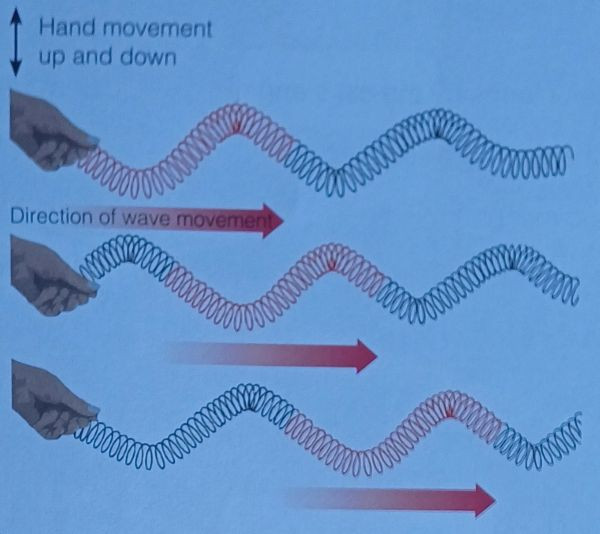
Key Features of Transverse Waves:

Oscillations: The particles move at right angles (perpendicular) to the direction of wave travel.

Examples: Light waves, water waves, and seismic waves (S-waves).

Wave Components:

• Crest: The highest point of the wave.
• Trough: The lowest point of the wave.

Transverse waves are commonly seen in water waves, electromagnetic waves (like light), and in some seismic waves (S-waves).

Longitudinal Waves

Longitudinal waves, in contrast, are waves in which the oscillations occur in the same direction as the wave travels. The particles of the medium move back and forth along the direction of wave motion, creating regions of compression and rarefaction.

Image

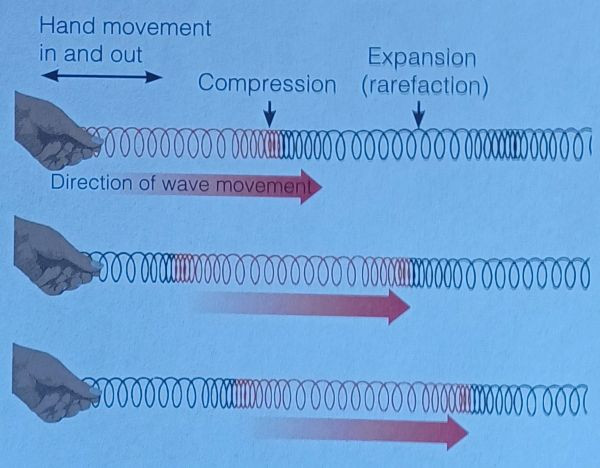
Key Features of Longitudinal Waves:

Oscillations: The particles vibrate in the same direction as the wave travels.

Examples: Sound waves in air, seismic waves (P-waves), and ultrasound waves.

Wave Components:

• Compression: The region where particles are closest together.
• Rarefaction: The region where particles are spread further apart.

Sound waves are the most common example of longitudinal waves, as they travel through gases, liquids, and solids by compressing and expanding the particles in the medium.

Wave Movement

Both transverse and longitudinal waves transfer energy without the transfer of matter. As a wave travels through a medium, the particles of the medium oscillate around their equilibrium position. In transverse waves, particles move perpendicular to the direction of energy transfer, while in longitudinal waves, they move parallel to it.

For example, in a water wave (transverse), the water rises and falls as the wave passes, but the water itself does not move forward. Similarly, in a sound wave (longitudinal), air molecules vibrate back and forth in the direction the wave travels, but the air itself does not move.

Properties of Waves

There are several key properties that are common to all waves, whether they are transverse or longitudinal:

• Amplitude: The maximum displacement of the particles from their rest position. It determines the energy and loudness of the wave (in sound waves) or the brightness (in light waves).
• Wavelength: The distance between two consecutive points in phase (e.g., crest to crest or trough to trough for transverse waves, or compression to compression for longitudinal waves).
• Frequency: The number of complete waves (or oscillations) that pass a point in one second. It is measured in hertz (Hz).
• Period: The time it takes for one complete wave to pass a given point. The period is the inverse of the frequency.
• Speed: The speed at which the wave travels through the medium. The speed of the wave depends on the medium through which it travels.

Wave Speed

The speed of a wave is defined as the distance travelled by a wave per unit of time. It is given by the equation:

$$\text{Wave Speed} (v) = \text{Frequency} (f) \times \text{Wavelength} (\lambda)$$ 

Where:

• v is the wave speed in metres per second (m/s),
• f is the frequency in hertz (Hz),
• λ (lambda) is the wavelength in metres (m).

For example, if a wave has a frequency of 5 Hz and a wavelength of 2 m, the wave speed is:

$$v = 5 \, \text{Hz} \times 2 \, \text{m} = 10 \, \text{m/s}$$

The wave speed can also be affected by the medium through which the wave is travelling. For example, sound waves travel faster in solids than in liquids or gases, and light waves travel faster in a vacuum than in air or glass.

Wave Speed Equation:

The relationship between wave speed (v), frequency (f), and wavelength (λ) is essential in understanding how waves behave. The equation is often written as:

$$v = f \times \lambda$$

Where:

• v is the wave speed (m/s),
• f is the frequency (Hz),
• λ is the wavelength (m).

This equation can be rearranged to solve for either frequency or wavelength if the other values are known. For example:

• To find the wavelength:
• To find the frequency:

$$\lambda = \frac{v}{f}$$

$$f = \frac{v}{\lambda}$$

Understanding wave speed and the relationship between wavelength and frequency is crucial in many applications, from telecommunications to medical imaging.

Summary

Waves are a fundamental concept in physics, and they come in two main types: transverse waves, where particles oscillate perpendicular to the wave direction, and longitudinal waves, where particles oscillate parallel to the wave direction. The key properties of waves include amplitude, wavelength, frequency, and speed. The wave speed equation $v = f \times \lambda$ allows us to relate these properties and solve problems involving waves.