Variations on a Theme

The method described here can be used to find the sum of any number of vectors by drawing an arrow for each vector, starting each new arrow where the previous one finished. The resultant of the vectors is then represented by the single arrow that starts at the beginning of the first vector and ends where the last one finishes.

If the vectors being added together form a closed figure, i.e. the last one finishes where the first one starts, it follows that the sum is zero. This is what you would expect to find when working out the resultant force at a point in a stable structure for example.

Image

For equilibrium at point X, the sum of the forces must be zero.

Although a scale drawing is often the quickest way of working out the resultant of two vectors, the size and direction can also be calculated. This is straightforward when the vectors act at right angles, but needs more complex mathematics in other cases.

In the worked example:

• the size of the resultant force can be calculated using Pythagoras’ theorem as √(2² + 3²) The notation ‘tan^-1’ means ‘the angle whose tangent is’.
• the angle between the resultant force and the 3 N force can be calculated using the definition of tangent as tan^–1 (2 ÷ 3).

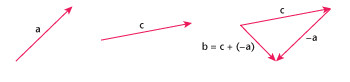
The method used to add two vectors is also used to subtract one vector from another. For example, an aircraft has velocity a and changes its velocity by an amount b so that its new velocity is c. The relationship between these vectors is a + b = c. To work out the change in velocity b, the relationship can be written as b = c – a, the new velocity – the old velocity. Vector b is found by adding (–a) to c. Vector –a is the vector equal in size to a but opposite in direction. Vector subtraction is illustrated in the diagram below.

Bold letters are used here to represent both the size and direction of a vector. When normal type is used, it represents the size of the vector only.

Image