Different types of Interaction

Objects moving in opposite directions
When two objects approach each other and collide head-on, the result of the collision depends on whether they stick together or whether one or both rebound. The diagram shows two ‘vehicles’ approaching each other on an air track. The vehicles join together and move as one.

Image

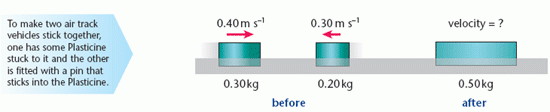
The principle of conservation of momentum can be used to work out the combined velocity, v, after the collision.

Image

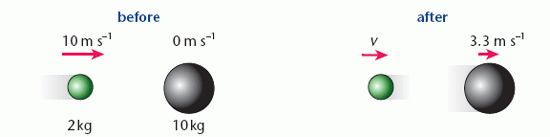
Taking velocity from left to right as being positive:
total momentum before collision =
0.3 kg × +0.4 m s^–1 + 0.2 kg × –0.3 m s^–1 = 0.06 N s.

This must equal the momentum after the collision, so 0.5 kg × v = 0.06 N s,
i.e. v = 0.12 m s^–1. As this is positive, it follows that the ‘vehicle’ is moving from left to right.

Rebound
When a light object collides with a heavier one, the light object may rebound, reversing the direction of its momentum. The diagram shows an example of such a collision.

Application of the principle of conservation of momentum in this case gives:
2 kg × 10 m s^–1 + 10 kg × 0 m s^–1 = 2 kg × v + 10 kg × 3.33 m s^–1
so 2 kg × v = 20 Ns – 33.3 Ns i.e. v = –6.7 m s^–1

The negative value means the object is moving from right to left.

The figures here are rounded. The 3.33 is a rounded value of 3 1?3.

Recoil

In some situations two objects are stationary before they interact, having a combined momentum of zero. After they interact, both objects move off but the combined momentum is still zero. Examples of this include:

• a stationary nucleus undergoes radioactive decay, giving off an alpha particle
• a person steps off a boat onto the quayside
• two ice skaters stand facing each other; then one pushes the other
• two air track vehicles fitted with repelling magnets are held together and then released.

When fire fighters use water to put out a fire, it often takes two people to hold the hose. This is due to the recoil as water is forced out of the nozzle at high speed.

In each case, both objects start moving from rest. For the combined momentum to remain zero, each object must gain the same amount of momentum but these momentum gains must be in opposite directions. The ice skater who does the pushing recoils as an equal and opposite force is exerted by the one who is pushed.

Image

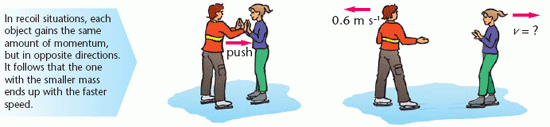
In the example shown in the above diagram, an 80 kg man pushes a 50 kg child.

Their combined momentum is zero both before and after this interaction.
Taking velocity from left to right as positive, this means that:
80 kg × – 0.6 m s–1 + 50 kg × v = 0
so v, the final velocity of the child, is 0.96 m s^–1 to the right.