Impulse
Jet and rocket engines are often working over a long period of time, so the second law written as force = rate of change of momentum can be readily applied when the time for which the force acts is not a fixed quantity. A manufacturer of aircraft engines, for example, uses the maximum force required to design the engine to achieve the required rate of output of exhaust gases.
A modern jet engine is capable of producing a force of 1 MN (1 × 106 N). Four of these engines are used to accelerate a jumbo jet to the speed required for take-off.
In situations where the time for which the force acts is known, or is short, the concept of impulse
can be more readily applied. The impulse of a force is the change in momentum that it causes. Using the concept of impulse, the second law can be written as:
impulse = force × time
= change in momentum
Impulse, like momentum, is measured in the equivalent units of N s or kg m s–1.
When tennis players or snooker players hit a ball, they are aware that the effect of the force that they exert depends on the time of contact with the ball as well as the size of the force. By maintaining contact with the ball over a longer period of time, a greater change in momentum can be caused by a given force.
When a child is taught how to catch a hard ball, he is shown how to pull back the hands while catching the ball. This extends the time required to stop the ball, so a smaller force is exerted on the hands.
In the example of a ball hitting a wall and rebounding, the force is not constant. It becomes greater as the ball becomes more compressed and decreases again as the ball returns to its original shape. The diagram below shows how the force on a ball changes during a collision with a wall.
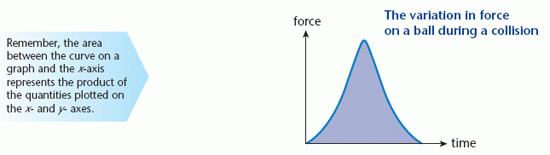
The impulse, or change in momentum of the ball, is represented by the area between the curve and the time axis, shown shaded on the graph.
Although the concept of impulse is often used to describe the effect of a force that acts over a short time, it can be applied to any interaction between objects. When a pole-vaulter lands on the ground, her momentum is typically 400 to 500 N s.
This is the size of the impulse needed to stop her. On a hard concrete surface she could be brought to rest in a tiny fraction of a second, needing a back-breaking force.
As impulse = force × time, the same change in momentum can be achieved by a smaller force acting over a longer time.
In practice sessions, longjumpers and highjumpers often land on a bed made of pieces of foam rubber. This gives a long ‘stopping’ time, so there is no chance of physical injury due to the impulse as they land.
