Momentum & the Second Law

Newton’s second law establishes the relationship between the resultant force acting on an object and the change of momentum that it causes. Important results that follow from the second law include F = ma, studied in force and acceleration, and the impulse of a force, to be met later in this section.

Newton’s second law states that:
The rate of change of momentum of an object is proportional to the resultant force acting on it and acts in the direction of the resultant force.
Δp/Δt α F

The expression Δp/Δt can be read as: change in momentum ÷ time taken for the change.

The definition of the newton (see force and acceleration) fixes the proportionality constant at 1. This enables the second law to be written as:

Force = rate of change of momentum
F = Δp/Δt

In this form, the second law is useful for working out the force in situations such as jet and rocket propulsion where the change in momentum each second can be calculated easily.

A rocket carries its own oxygen supply, so that it can fire the engines when it is travelling in a vacuum. A spacecraft travelling where it is not affected by any gravitational fields or resistive forces maintains a constant velocity, so it only needs to fire the rocket engines to change speed or direction.

The principle of rocket propulsion can be seen by blowing up a balloon and letting it go; the air squashed out of the neck of the balloon gains momentum as it leaves, causing the balloon and the air that remains inside to gain momentum at the same rate but in the opposite direction. The diagram shows the principle of rocket propulsion.

Jet and rocket engines use the same principle; hot gases are ejected from the back of the engine to provide a force in the forwards direction. The difference is that jet engines are designed to operate within the Earth’s atmosphere, so they can take oxygen from their surroundings.

Image

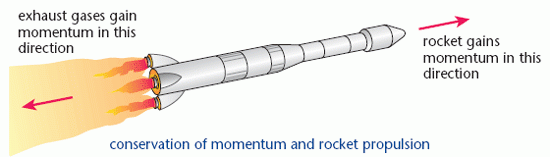
In this example, the exhaust gases are emitted at a rate of 3000 kg s^–1. The speed of the exhaust gases relative to the rocket is 1500 m s^–1. The rate of change of momentum of these gases is therefore 4 500 000 kg m s^–2, i.e. 4 500 000 kg m s–1 each second. This is the size of the force on both the gases and the rocket.

The unit kg m s^–2 is equivalent to the N, so a rate of change of momentum of 4 500 000 kg m s^–2 is another way of stating: a force of 4 500 000 N.