Speed-Time & Velocity-Time graphs

Any object that is changing its speed or direction is accelerating. Speeding up, slowing down and going round a corner at constant speed are all examples of acceleration. Acceleration is a measure of how quickly the velocity of an object changes.

Instantaneous acceleration = rate of change of velocity. It is represented by the gradient of a velocity–time graph.
average acceleration = change in velocity ÷ time a = Δv ÷ Δt
Acceleration is a vector quantity and is measured in m s^–2.

In physics, any change in velocity is an acceleration. This means that an object moving at constant speed, but changing direction, is accelerating.

Speed–time and velocity–time graphs both give information about the motion of an object that is accelerating. The graphs below both represent the motion of a ball after it has been thrown vertically upwards with an initial speed of 15 m s^–1.

Image

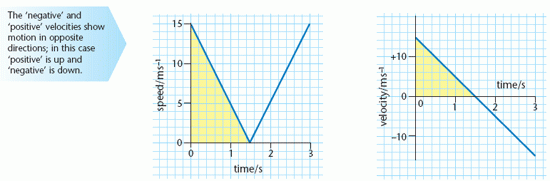
The speed–time graph shows that the speed decreases to zero as the ball reaches its maximum height and then increases. The velocity–time graph also shows the change in direction of the ball. In each case the gradient of the graph is numerically equal to the acceleration (as the ball is moving vertically this is free-fall acceleration), but the gradient of the velocity–time graph also shows that the direction of the acceleration (vertically downwards) is opposite to that of the initial velocity.

The distance that the ball travels in any time interval can also be obtained from the graphs. Since distance travelled = average speed × time, this is represented by the area between the curve and the time axis. The area that represents the distance travelled by the ball while moving upwards is shaded on each graph.

Remember, the area of a triangle = 1?2 × base × height.

The gradient of a velocity–time graph represents the acceleration.
The area between the curve and the time axis of a velocity–time or a speed–time graph represents the distance travelled.

Check that the shaded area represents a distance of 11.25 m in each case.